MOMEN GAYA,MOMEN KOPEL,MOMEN INERSIA

Momen gaya,momen kopel,dan momen inersia hanya berlaku pada benda tegar.
Apa itu benda tegar??
     Benda tegar yaitu benda yang tidak mengalami perubahan bentuk ketika suatu gaya dikerjakan padanya 

Nah dalam blog kali ini kita akan membahas beberapa hal yang berkaitan dengan rotasi benda tegar apa aja itu?? 
Yuk, check it down !!! 

1. Momen gaya 
 Nah apasih itu momen gaya? 
Momen gaya itu adalah hasil perkalian silang antara vektor posisi titik kerja gaya terhadap poros(r) dengan vektor gaya (F) 
  Apasih rumus nya untuk mencari itu?        Torsi atau momen gaya dirumuskan dengan:

Ket :
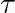 adalah torsi atau momen gaya (Nm)
r adalah lengan gaya (m)
F adalah gaya yang diberikan tegak lurus dengan lengan gaya (N)

Jika gaya yang bekerja pada lengan gaya tidak tegak lurus, maka besar torsinya adalah:

dimana 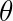 adalah sudut antara gaya dengan lengan gaya.

Contoh soal : 
Batang AC = 4 m dengan poros titik A dengan gaya F1sebesar 20 N dan F2 sebesar 12 N. Sudut-sudut ditunjukkan gambar berikut: 

 

Jika titik B berada di tengah tentukan momen gayanya nah 
massanya di abaikan 

Pembahasan
Momen gaya dengan poros di titik A:
τ = F1 AC sin 60° − F2 AB sin 60° 
τ = 20 (4) (1/2 √3) − 12 (2) (1/2 √3) 
τ = 28√3 Nm

2. Momen kopel 
Nah sekarang kita akan membahas tentang momen kopel, apa itu momen kopel? Apasih bedanya sama momen gaya? 
Nah perbedaan nya itu kalo momen gaya dia pakai gaya yg tidak sama besar 
Tapi kalau momen kopel yaitu pasangan dua buah gaya yg sama besar,mempunyai garis kerja yang sejajar dan arahnya berlawanan. 

Rumus untuk mencari momen kopel : 

                     M = Fd 
Ket : M = momen kopel (Nm) 
         F  = gaya (N) 
         d  = lengan kopel (m ) 

Nah ada kentuan untuk menentukan momen kopel tersebut bernilai positif(+) atau negatif (-) bisa kita liat pada gambar ya!! 

Contoh soal : 

Sesuai pada gambar tentukan momen kopel nya jika diketahui F1=F2= 30N dan lengan kopel (d) = 5m

Penyelesaian : 

Dik : F1=F2= 30N 

         d = 5m 

Dit : M...? 

Jawab : M = Fd 

                   = 30 N . 5 m 

                   = 150 Nm 

Gampang kan 👌😜

3.Momen inersia 

Momen inersia adalah hasil kali massa partikel dengan kuadrat jarak partikel terhadap sumbu porosnya. 
Secara umum jika jenis bendanya tidak di ketahui maka rumusnya : 
                      

                                I = m₁R₁² +m₂R₂² + m₃R₃² +…+m_nR_n²

Tetapi jika benda nya di ketahui maka ada 9 rumus momen inersia benda tegar homongan, check on bellow 👌👌 : 

Contoh soal 1 :
(Contoh yg tidak di spesifikkan bendanya)
1) Dik : m1 = 1 kg, m2 = 2 kg, m3 = 2 kg, m4 = 1 kg, dan r1=r2=r3=r4= 20 cm. 
Dit : maka hitung lah momen inersia sistem 
Jawab : 
                  I = m1R1 ² + m2R2²+ m3R3² + m4R4²

= (1 kg)(0,2 m)²+ (2 kg)(0 m)² + (2 kg)(0,2 m)²+ (1 kg)(0,4 m)² = 0,28 kgm²

^{Contoh soal 2 :} 

^{(Contoh yg di spesifikkan bendanya)} 

^{Diketahui sebuah batang homongen(poros melalui pusat) memiliki massa(m) = 6 kg dan L = 2 m maka hitung lah momen inersia benda tersebut!} 

^{Jawab :} 

                 ^{I= 1/12mL^2} 

                   ^{= 1/ 12 (6kg)(2m)^2} 

                   ^{= 2 kgm^2} 

^{2) Diketahui sebuah benda silindris tipis berongga memiliki massa(m) = 10kg dan jari-jari (r) = 2m maka hitunglah momen inersia benda tersebut} 

^{Jawab :} 

                ^{I = mr^2} 

                  ^{= (10kg)(2m)^2} 

                  ^{=40 kgm^2}